In this governor, balls are connected by a spring (in two parts) and one more spring is used in sleeve mechanism to adjust the radius of rotation of the balls as shown in Figure 14.8.
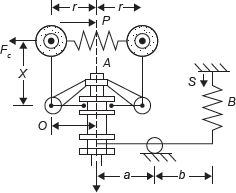
Figure 14.8 Willson–Hartnell Governor
Let
P = Tension in the main spring A
S = Tension in spring B
w = Weight of each ball
W = Weight of sleeve
sa = Stiffness of each ball spring A
sb = Stiffness in auxiliary spring B
FC = Centrifugal force on each ball
r = Radius of rotation of balls
Taking moment about O neglecting weight of ball, we get
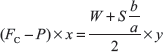
Using 1 and 2 suffix for minimum and maximum equilibrium speed
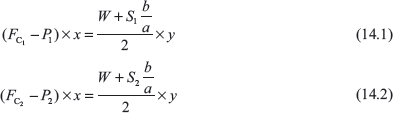
On subtraction, we get
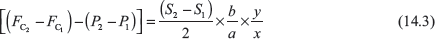
When the radius of rotation increases from r1 to r2, the spring A extends by 2 (r2 − r1) and spring B extends by (r2 − r1) × ![]() .
.
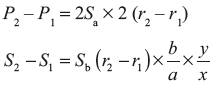
Substituting the value of P2 − P1 and S2 − S1 in Eq. (14.3)
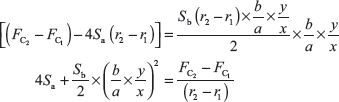
Example 14.6: A Wilson–Hartnell governor consists of balls of mass of 2 kg each, minimum and maximum radius of rotation 150 and 180 mm, respectively, minimum and maximum speed 220 and 240 rpm, respectively, length of ball arm of each bell crank lever 150 mm, length of the sleeve arm of each bell crank lever 100 mm, and combined stiffness of two ball springs 0.2 kN/m. Find the equivalent stiffness of the auxiliary spring referred to the sleeve.
Solution:
Let S be the equivalent stiffness of the auxiliary spring referred to the sleeve, ![]()
We know the centrifugal force at the minimum speed,
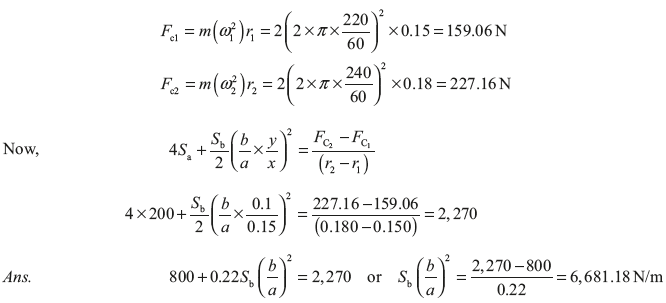
Leave a Reply