Figure 13.12 shows the schematic diagram of double purchase winch crab. In this device, velocity ratio is increased by using two pairs of gears. There are three axles as effort axle, intermediate, and load axle, two pinion gears as P1 and P2, two spur gears as S1 and S2. Pinion P1 mounted on effort axle, pinion P2 and spur gear S1 are mounted on the intermediate axle while spur gear S2 is mounted on load axle.
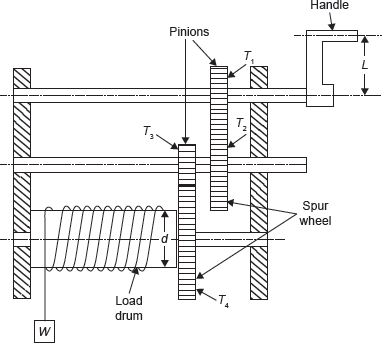
Figure 13.12 Double Purchase Winch Crab
Weight W is attached to the string wound on the load axle while the effort is applied on the lever arm of the effort axle. Hence by rotating the lever, the pinion is rotated, which rotates the spur gear and pinion on intermediate shaft, the pinion on intermediate axle rotates the gear on load axle; in this way load W gets lifted.
When the lever arm rotates by one revolution, the effort axle and pinion P1 also moves by one revolution = 2πL
As we know,

The load axle S2 rotates by, ![]() revolution
revolution
Hence, the distance moved by load ![]()
Distance moved by effort axle = 2πL
where T1 is number of teeth on pinion P1, T2 is number of teeth on spur gear S1, T3 is number of teeth on pinion P2, T4 is number of teeth on spur gear S2, L is length of lever arm, and r is radius of load axle.
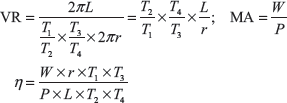
Example 13.12: In a double purchase winch crab, the pinions have 15 and 45 teeth while spur wheels contain 60 and 90 teeth. The effort handle is 500 mm long while the effective diameter of the drum is 180 mm. If the efficiency of the winch is 45%, find the load that can be lifted with an effort of 125 N applied at the end of the handle.
Solution:
Given: T1 = 15, T3 = 45, T2 = 60, T4 = 90, L = 500 mm, r = 90 mm
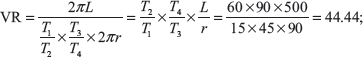
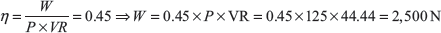
Example 13.13: A double purchase winch crab has the following specifications:
Effective diameter of load drum = 160 mm
Length of handle = 360 mm
Number of teeth on pinions = 20 and 30
Number of teeth on spur wheels = 75 and 90
When tested it was found that an effort of 90 N was required to lift a load of 1,800 N and an effort of 135 N was required to lift a load of 3,150 N. Determine (i) law of machine, (ii) probable effort to lift a load of 5,000 N, and (iii) efficiency in the above case.
Solution:
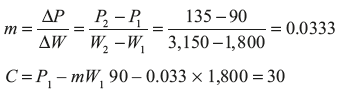
- Law of machine, P = 0.033W + 30
- P3 = mW3 + C or P3 = 0.033 × 5,000 + 30 = 196.5 N

Leave a Reply