Condition for Irreversibility or Self-locking of Machine

In the case of self-locking machine, after load removal friction force overcomes the work done by the load in reverse direction.

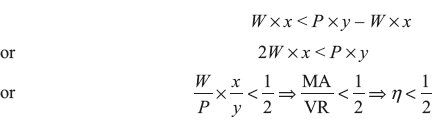
Thus for an irreversible of self-locking machine efficiency should be less than 50%.

Example 13.1: In a lifting machine, it was found that the effort was moved by 300 mm to lift a load by 10 mm. This machine is used to lift a load of 50,000 N by an effort of 2,000 N. Determine (i) velocity ratio, (ii) mechanical advantage, (iii) efficiency, (iv) ideal effort, (v) effort lost in friction, (vi) the load which could have been lifted with the given effort under the ideal conditions, and (vii) friction of the machine.

Solution:

1. 
2. 
3. 
4. 
5. Effort lost in friction = Actual effort – Ideal effort = 2,000 – 1,666.66 = 333.33 N
6.  
7. Friction of machine = Ideal load – Actual load = 60,000 – 50,000 = 10,000 N

Example 13.2: In a lifting machine, an effort of 100 N raised a load of 1,000 N and an another effort of 500 N raised a load of 6,000 N. Find (i) law of machine, (ii) effort required to lift a load of 8,000 N, and (iii) maximum mechanical advantage.

Solution:

Let P be the effort, W be the load, and m be the slope of the graph as shown in Figure 13.4.

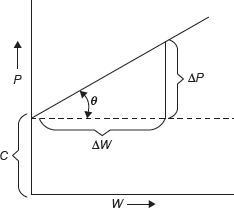
Figure 13.4 Law of Machine

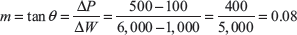
1. Law of the machine, C can be determined from first or second loading conditions of the question.
2. P = 0.08W + 20 = 0.08 × 8,000 + 20 = 660 N
3. Maximum mechanical advantage 

Example 13.3: In a lifting machine, an effort of 1 kN was required to lift a load of 30 kN, the velocity ratio of the machine being 50. Is the machine reversible? If so what effort can be removed so that the machine is at the point of reversing?

Solution:

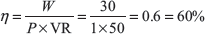
Since the efficiency is more than 50%, the machine is reversible.

Ideal load that can be lifted with an effort of 1 kN.

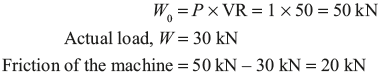
Example 13.4: In a lifting machine, the effort required to lift loads 200 N and 300 N were 50 N and 60 N, respectively. If the velocity ratio of the machine is 20, determine (i) law of machine, (ii) efficiencies corresponding to loads of 200 and 300 N, (iii) effort lost in friction in both the cases, and (iv) the maximum efficiency which can be expected from the machine.

Solution:

1.   
2.   
3.  Effort lost in friction for 200 N load, P_f200 = 50 – 10 = 40 NEffort lost in friction for 300 N load, P_f300 = 60 – 30 = 30 N
4.