Modulus of rigidity (G) is the ratio of shear stress (τ) and shear strain (γ).
Let us consider an elemental cube ABCD be subjected to a simple shear stress τxy as shown in Figure 12.24 (a). An equivalent system with principal stresses τxy and –τxy are acting along the diagonals as shown in Figure 12.24 (b). The distorted condition of the cube is shown in Figure 12.24 (c).
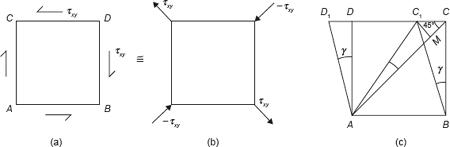
Figure 12.24 Shear Stress and Strain on a Cube of Unit Length
Draw C1M perpendicular to AC and join AC1
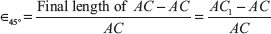
Also, AC1 = AM (since γ is small)
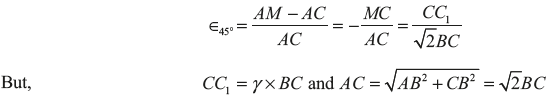

Now, ∈45° can also be found by referring to the equivalent system of Figure 12.24 (b) as
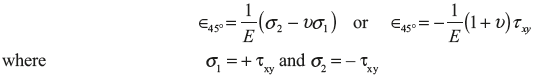
From Eq.(12.7)
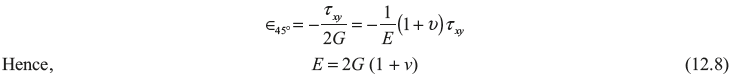
From Eq. (12.6) in previous section and Eq. (12.8)
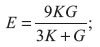
Relationship among E, K, and G.
Example 12.13: A bar of 50 mm diameter is subjected to a load of 100 kN. The measured extension on the gauge length of 250 mm is 0.12 mm and the change in diameter is 0.0040 mm. Calculate Poisson’s ratio, volumetric strain, and value of three moduli of elasticity.
Solution:


Example 12.14: For a given material, Young’s modulus is 110 GN/m2 and shear modulus is 42 GN/m2. Find the bulk modulus and lateral contraction of a round bar of 37.5 mm diameter and 2.4 m long when stretched by 2.5 mm.
Solution:
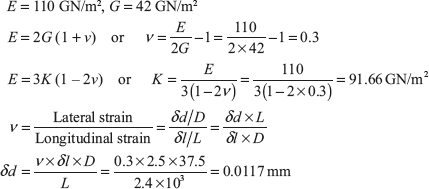
Example 12.15: A bar 2 cm × 4 cm in cross-section and 40 cm long is subjected to an axial tensile load of 70 kN as shown in Figure 12.25. It is found that the length increases by 0.175 mm and lateral dimension of 4 cm decreases by 0.0044 mm. Find (i) Young’s modulus, (ii) Poisson’s ratio, (iii) Change in volume of the bare, and (iv) Bulk modulus.
Solution:
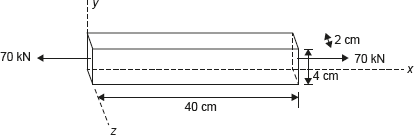
Figure 12.25 A Rod Under Tensile Load
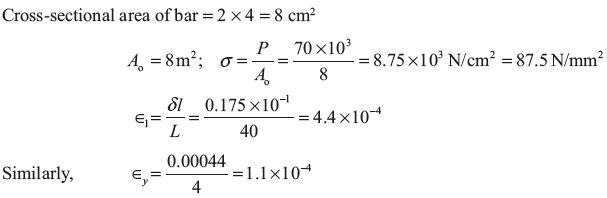


Leave a Reply