Velocity triangle for Francis turbine is shown in Figure 9.12.
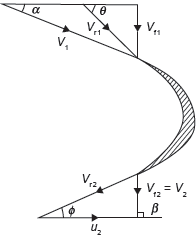
Figure 9.12 Velocity Triangle for Francis Turbine
Here,
- V1 and V2 are velocities of jet at inlet and outlet, respectively;
- Vr1 and Vr2 are relative velocities of jet with respect to bucket at inlet and outlet, respectively;
- u1 and u2 are bucket velocities at inlet and outlet, respectively;
- Vf1 and Vf2 are velocities of flow, i.e., component of V1 and V2 in the direction of motion of bucket at inlet and outlet, respectively;
- Vω1, and Vω2 are velocities of whirl at inlet and outlet, respectively;
- α is an angle between direction of jet and direction of motion of bucket;
- θ is an angle between Vr1 and direction of motion of bucket;
- β is an angle between V2 and direction of motion of bucket; and
 is an angle between Vr2 and direction of motion of bucket.
is an angle between Vr2 and direction of motion of bucket.
The work done per second on runner by water,
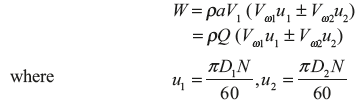
The work done per second per unit weight of water = ![]()
where +ve sign is taken if β < 90; −ve sign is taken if β > 90, and Vω2 = 0, if β = 90.
In case of Francis turbine β = 90
Now, work done per second per unit weight of water = ![]()
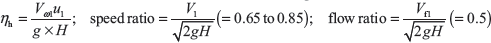
Example 9.8: A Francis turbine working under a head of 8 m. The overall efficiency is 70% and power required to produce 150 kW. The peripheral and radial velocities at inlet are 0.3 ![]() and 0.96
and 0.96 ![]() , respectively. The wheel runs at 160 rpm and hydraulic efficiency of the turbine is 78%. Assuming radial discharge, find (i) the guide blade angle, (ii) vane angle at inlet, (iii) diameter of the wheel at inlet, and (iv) width of the wheel at inlet.
, respectively. The wheel runs at 160 rpm and hydraulic efficiency of the turbine is 78%. Assuming radial discharge, find (i) the guide blade angle, (ii) vane angle at inlet, (iii) diameter of the wheel at inlet, and (iv) width of the wheel at inlet.
Solution:
Given:
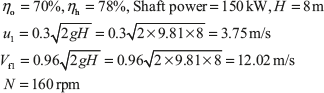
There is radial discharge at outlet, therefore Vω2 = 0 and Vf2 = V2
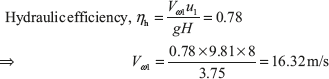
- Guide bladeangle, α

- Wheel vane angle at inlet, θ

- Diameter of wheel at inlet, D1

- Width of the wheel at inlet, b1

Example 9.9: An inward flow reaction turbine rotates at 360 rpm. The wheel vanes are radial at inlet and inner diameter of wheel is one third of the outer diameter. The constant velocity of flow in the wheel is 2.5 m/s. Water enters the wheel at an angle of 15° to the tangent at the wheel at inlet. The width of wheel at inlet is 90 mm and area of flow blocked by vane is 2% of the gross area of flow at inlet. Assuming radial discharge, find (i) head available, (ii) vane angle at outlet, (iii) the outer and inner diameter of wheel, and (iv) the theoretical water power developed by the wheel.
Solution:
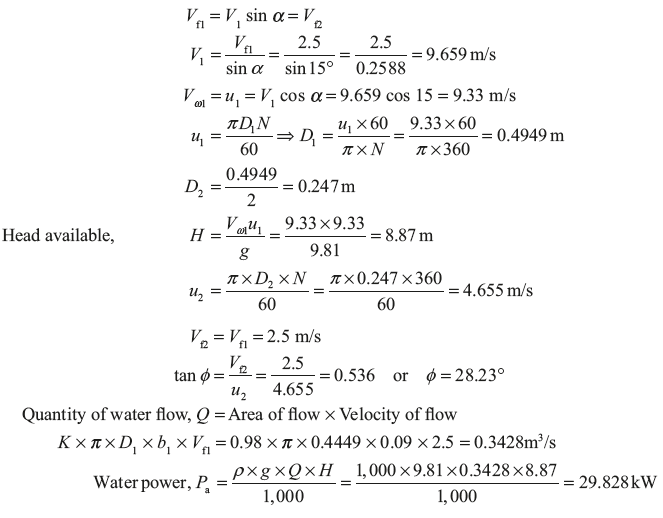
Leave a Reply