Here,
- V1 and V2 are velocities of jet at inlet and outlet, respectively;
- Vr1 and Vr2 are relative velocities of jet with respect to bucket at inlet and outlet, respectively;
- u1 and u2 are bucket velocities at inlet and outlet, respectively;
- Vf1 and Vf2 are velocities of flow, i.e., component of V1 and V2 in the direction of motion of bucket at inlet and outlet, respectively;
- Vω1 and Vω2 are velocities of whirl at inlet and outlet, respectively;
- α is an angle between direction of jet and direction of motion of bucket;
- θ is an angle between Vr1 and direction of motion of bucket;
- β is an angle between V2 and direction of motion of bucket; and
- ɸ is an angle between Vr2 and direction of motion of bucket.
In the case of Pelton wheel, α = 0, θ = 0, u1 = u2 = u = πDN/60, V1 = Vω1, Vr1 = V1 − u1 = V1 − u where D is diameter of wheel and N is rpm.
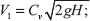
where H is net head equals to Hg − Hf.
Hg and Hf is gross and friction heads, respectively, Cv is co-efficient of velocity.
From Velocity Triangle (in Figure 9.8b)
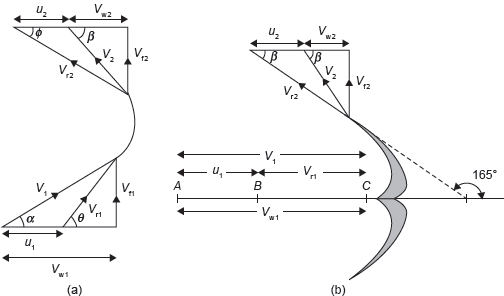
Figure 9.8 (a) Velocity Triangle for Series of Radial Vane, and (b) Velocity Triangle for Pelton Turbine
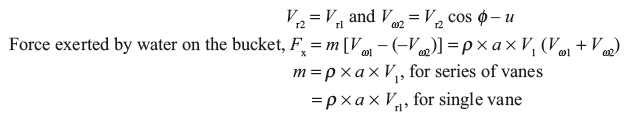

For maximum efficency, 
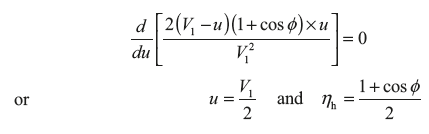
Example 9.6: A Pelton turbine is coupled with an electric generator of 10,000 kW. The head of water available at nozzle is 800 m. Assuming generator efficiency as 95%, Pelton wheel efficiency as 85%, co-efficient of velocity for nozzle as 0.96, speed ratio as 0.36, jet deflection angle by the bucket as 165° and relative velocity at outlet as 0.95 times that of inlet, calculate (i) diameter of jet, (ii) flow of water in m3, and (iii) force exerted by jet on bucket. If ratio of bucket diameter to jet diameter is 10, find the synchronous speed for generation at 50 cycles per second and the corresponding mean diameter of the runner.
Solution:
Given: P = 10,000kW; H = 800m; ηgen = 0.95; ηt = 0.85; Cv = 0.96; Cu = 0.36; ɸ = 180 − 165 = 15 Vr2 = 0.95 Vr1; D/d = 10; f = 50 cycles/s
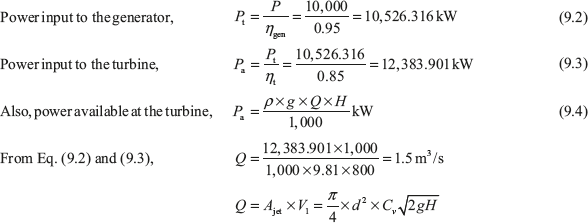

Frequency of generator,![]() , where P is number of pairs of poles and N is synchronous speed.
, where P is number of pairs of poles and N is synchronous speed.
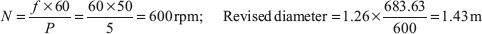
Example 9.7: A Pelton wheel is to be designed with following specifications: Shaft power = 12,000 kW, Head = 400 m, Speed = 800 rpm, Overall efficiency = 86%, jet diameter is one tenth of wheel diameter. Determine (i) the wheel diameter, (ii) the number of jets required, and (iii) diameter of jet. Assume Cv = 0.98 and Cu = 0.45.
Solution:
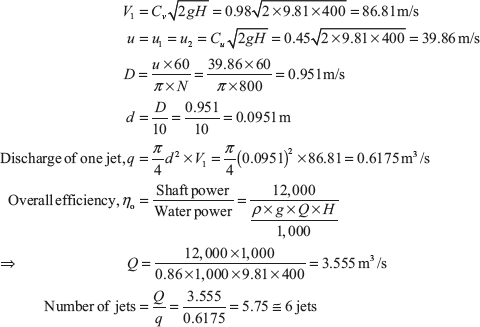
Leave a Reply