The interaction of the static fluid with its surroundings is in the form of force, which is applied equally on all contact points. This force is the result of the pressure applied on a particular unit area. The pressure in the fluid is not constant throughout. The pressure in any body of fluid varies with depth and it increases with the depth of the fluid. But at the same level relative to the vertical direction the pressure will be same in the fluid. The increase in pressure as we go down the fluid is due to the weight of the fluid column above that level.
The variation of the pressure with depth of the liquid column can be formulated with this simple analysis. Consider a vertical column of a liquid with a constant cross-sectional area. The liquid under consideration is at rest so there is no shear forces acting or coming in to picture. The liquid column is in equilibrium so all the forces are balanced in the column. At any point in the column net force is zero. The weight of the column at any particular depth is balanced by the force due to pressure at that point. Thus, the pressure at that point is equal to the weight of the column at that point divided by the area of cross section of the liquid column.
Let P denote the pressure at the base of the cylinder; since p changes at a rate 
with elevation, the pressure is found from the definition of a derivative to be
at the top of the cylinder. (Note that we do not anticipate a reduction of pressure with elevation here; hence, the plus sign is used. If, indeed—as proves to be the case—pressure falls with increasing elevation, then the subsequent development will tell us that is negative). Hence, the fluid exerts an upward force of pA on the base of the cylinder and a downward force of 
A on the top of the cylinder (Refer Figure 9.4).
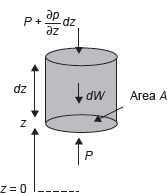
Figure 9.4 Forces Acting on Cylinder of Fluid
Next, apply Newton’s second law of motion by equating the net upward force to the mass times the acceleration which is zero, since the cylinder is stationary:
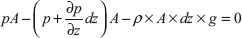
Cancellation of PA and division by Adz leads to the following differential equation, which governs the rate of change of pressure with elevation:
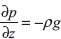
Note: Pressure at the depth h in a fluid of density ρ may be given as: P = P0 + ρ × g × h, where P0 is pressure at the open surface of the fluid.
Leave a Reply