Heat Transfer Through Hollow Cylinder

Consider a cylinder of internal radius r₁ and external radius r₂ as shown in Figure 7.7. Let the inside and outside temperatures be t₁ and t₂, respectively. Consider the heat flow through a small element of thickness dr at any radius r, where the temperature is t. Let the thermal conductivity of the material be k, temperature of fluid flow inside the cylinder be t_f1, heat transfer coefficient be h_f1, temperature of fluid flow outside the cylinder be t_f2 and heat transfer coefficient be h_f2. The heat transfer through the elemental area of length l can be given by,

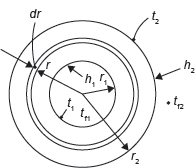
Figure 7.7 Heat Transfer Through Cylindrical Wall

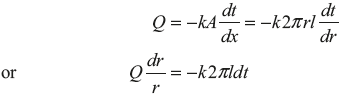
Integrating between the inside and outside surfaces,

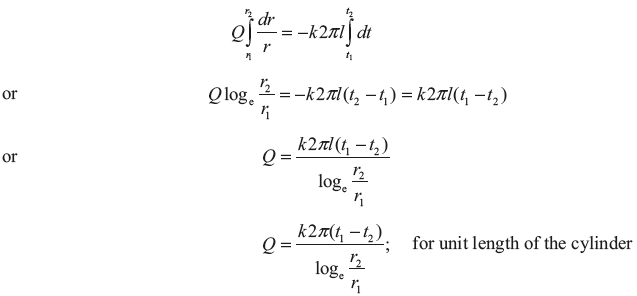
If we put mean area A_m and mean radius r_m in the above equation as

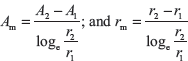
In the case of a composite cylinder the most convenient approach is again that of the electrical analogy; by using where x is thickness of a layer and A_m is the logarithmic mean area for that layer.

The film of fluid on the inside and outside surfaces can be treated as

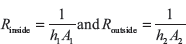
Example 7.5: A steel pipe of 80 mm bore and 8 mm wall thickness, carrying steam at 250°C, is insulated with 36 mm of a moulded high temperature diatomaceous earth covering. This covering is in turn insulated with 50 mm of asbestos felt. If the atmospheric temperature is 20°C, calculate the rate at which heat is lost by the steam per metre length of pipe. The heat transfer coefficients for the inside and outside surfaces are 525 and 27 W/m²K, respectively, and the thermal conductivity of steel, diatomaceous earth and asbestos felt are 55, 0.1 and 0.08 W/m K, respectively. Calculate also the temperature of the outside surface.

Solution:

Given: r_i = 40mm; r₁ = 48mm; r₂ = 84mm; r₀ = 134mm; h₁ = 525 W/m²K; m²K

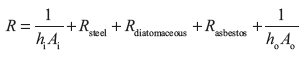
Now resistance of per unit length of pipe