Combined Heat Transfer

Plane Walls with Convection on Sides

There are many cases in practice when different materials are constructed in layers to form a composite wall. This wall may be composed of plaster layer, brick layer, tiles layer, etc. as shown in Figure 7.3.

In Figure 7.3 there are three layers A, B, C, of thickness L_A, L_B, and L_C, respectively. The thermal conductivities of the layers are k_A, k_B, and k_C. On one side of the composite wall there is a fluid at temperature t_∞1 and heat transfer coefficient from fluid to wall is h₁; on other side of the composite wall there is fluid at temperature t_∞2 and the heat transfer coefficient from fluid to wall is h₂. Let the temperature of the wall in contact with fluid on one side is t₁ and on other side t₄. The interface temperatures of the composite wall are t₂ and t₃. To solve the heat flow problem an analogous of electrical current may be used. The heat flow is caused by temperature difference whereas the current flow is caused by a potential difference. Hence, it is possible to postulate a thermal resistance analogous to an electrical resistance. From Ohm’s law we have, V=IR or I=V/R, where V is potential difference, I is current and R is resistance.

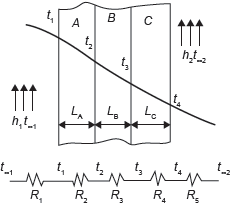
Figure 7.3 Plane Walls with Convection on Sides

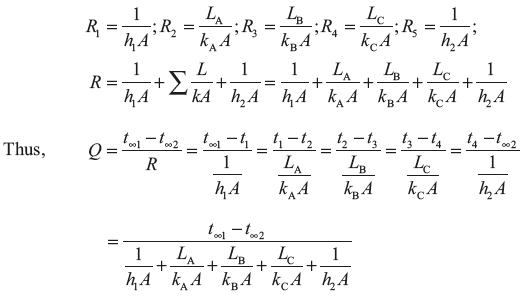
Thermal resistance,  and thermal resistance for a fluid film,  where Q is analogous to I and Δt is analogous to ΔV.

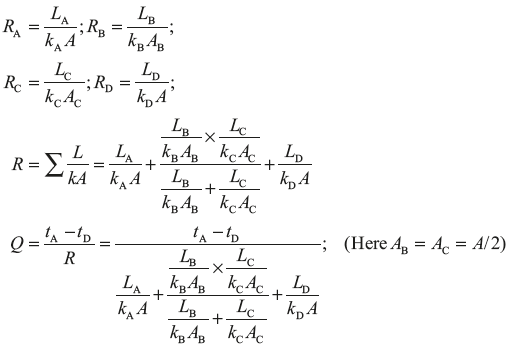
Example 7.2: Derive the expression for the heat transfer through series and parallel composite walls as shown in Figure 7.4.

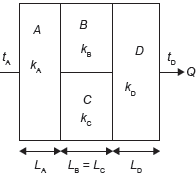
Figure 7.4 Heat Transfer Through Composite Wall

Solution:

The electrical current analogy of the heat transfer is shown in Figure 7.5.

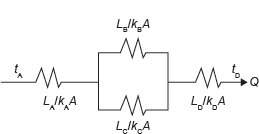
Figure 7.5 Electrical Analogy of Heat Transfer for Composite Wall is Shown in Figure 7.4

Example 7.3: A steel tank of wall thickness 8 mm contains water at 80°C. Calculate the rate of heat loss per m² of tank surface area when the atmospheric temperature is 20°C. The thermal conductivity of mild steel is 50 W/m K, and the heat transfer coefficients for the inside and outside of the tank are 2,500 and 20 W/m²K, respectively. Calculate also the temperature of the outside surface of the tank.

Solution:

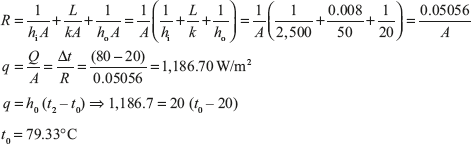
Example 7.4: A furnace wall consists of 120 mm thick refractory brick and 120 mm thick insulating firebrick separated by an air gap as shown in Figure 7.6. The outside wall is covered with a 10 mm thickness of plaster. The inner surface of the wall is at 1,000°C and the room temperature is 20°C. Calculate the rate at which heat is lost per m² of wall surface. The heat transfer coefficient from the outside wall surface to the air on the room is 20 W/m²K, and the resistance to heat flow of the air gap is 0.15 K/W. The thermal conductivity of refractory brick, insulating firebrick and plaster are 1.6, 0.3 and 0.14 W/m K, respectively. Calculate also each interface temperature of the outside of the wall.

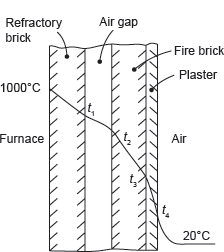
Figure 7.6 Composite Walls

Solution:

Given: