In the impulse turbine, all the pressure drops occur in nozzle and there is no pressure drop of steam passing through blades. Let us consider steam enters the nozzle with pressure of P0 and velocity of V0, after expansion of steam in nozzle pressure drops to P1 and velocity increases to V1. High velocity jet of steam impinges on the blades with velocity V1 gets deflected by an angle and comes out with smaller velocity V2 producing an impulse on the blades. The pressure P1 remains constant passing through the blades.
Now, momentum at the inlet of the blade – Momentum at the exit of the blade = Impulse on the blade absorbed in producing shaft work.
After expansion of steam in nozzle, it strikes the blades with absolute velocity V1 which rotates the blade with mean peripheral velocity u, steam leaves the blade with relative velocity Vr2 and absolute velocity V2 as shown in Figure 5.9.

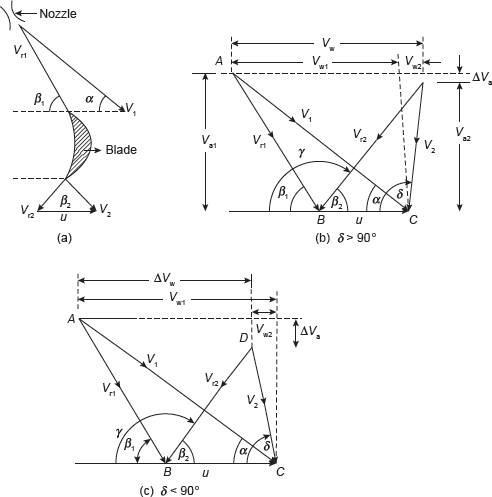
Figure 5.9 Velocity Diagram for Impulse Turbine
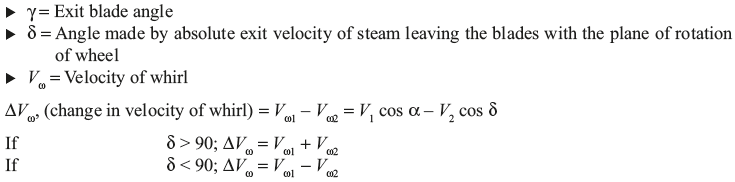
In Figure 5.9b, in ΔABC
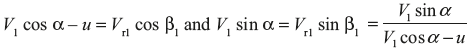
In ΔCBD
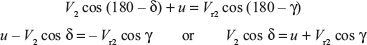
Similarly, in Figure 5.9c
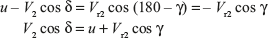
Blade Friction Factor: It is ratio of relative velocity of steam at exit to the relative velocity at inlet of the blade. It is denoted by Kb
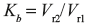
Energy loss due to friction in blade
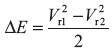
In terms of Kb, ΔVω = (V1 cos α – u) (1 + Kb); if blade are symmetrical, i.e., β1 = β2
Tangential Thrust
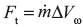
Axial Thrust
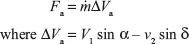
Blade Work or Diagram Work
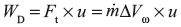
Input energy to the blade = ![]()

Maximum Blade Efficiency and Optimum Velocity Ratio: Substituting ΔVω in equation of blade efficiency
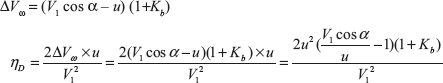
Velocity ratio is the ratio of mean velocity of blade to the jet velocity
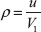
as
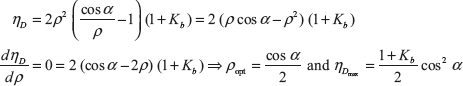
Putting the value of ρ as ![]() and if loss of energy due to friction is zero, i.e., Kb = 1
and if loss of energy due to friction is zero, i.e., Kb = 1
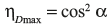
Thus, lower is the nozzle angle, higher is the blade efficiency. But, too low nozzle angle causes energy loss at the blade inlet. Therefore, the nozzle angle is to be maintained within certain range which varies from 16° to 22°.
Example 5.1: Steam enters an impulse turbine at 1,000 m/s and at a nozzle angle of 18°. The mean peripheral velocity of blades is 600 m/s and blades are symmetrical. If the steam is to enter the blades without shock, what will be the blade angles?
- If friction effect is negligible on the blades, calculate the tangential thrust on the blades and diagram power for unit mass flow rate of steam.
- If blade friction (Kb) is 0.8, estimate the axial thrust, diagram power and diagram efficiency.
Solution:
Velocity triangle is shown in Figure 5.10.
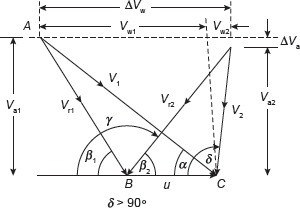
Figure 5.10 Velocity Triangle
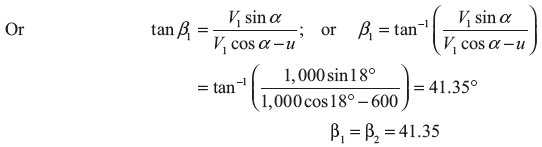



Leave a Reply