Real Gas Law

The behavior of natural gas mixtures can be approximated by the real gas law

where Z is the compressibility factor, also called the gas deviation factor in the petroleum engineering literature. The universal gas constant, R, is equal to 10.73 psi ft³/lb-mol-°R. Equation (4-2) is a general equation of state for gases. The gas compressibility factor for mixtures of hydrocarbon gases can be obtained from Figure 4-1 (Standing and Katz, 1942). This well-known graph was constructed for hydrocarbon gas mixtures. In the presence of large amounts of nonhydrocarbon gases, the gas compressibility factor must be adjusted, as is demonstrated.

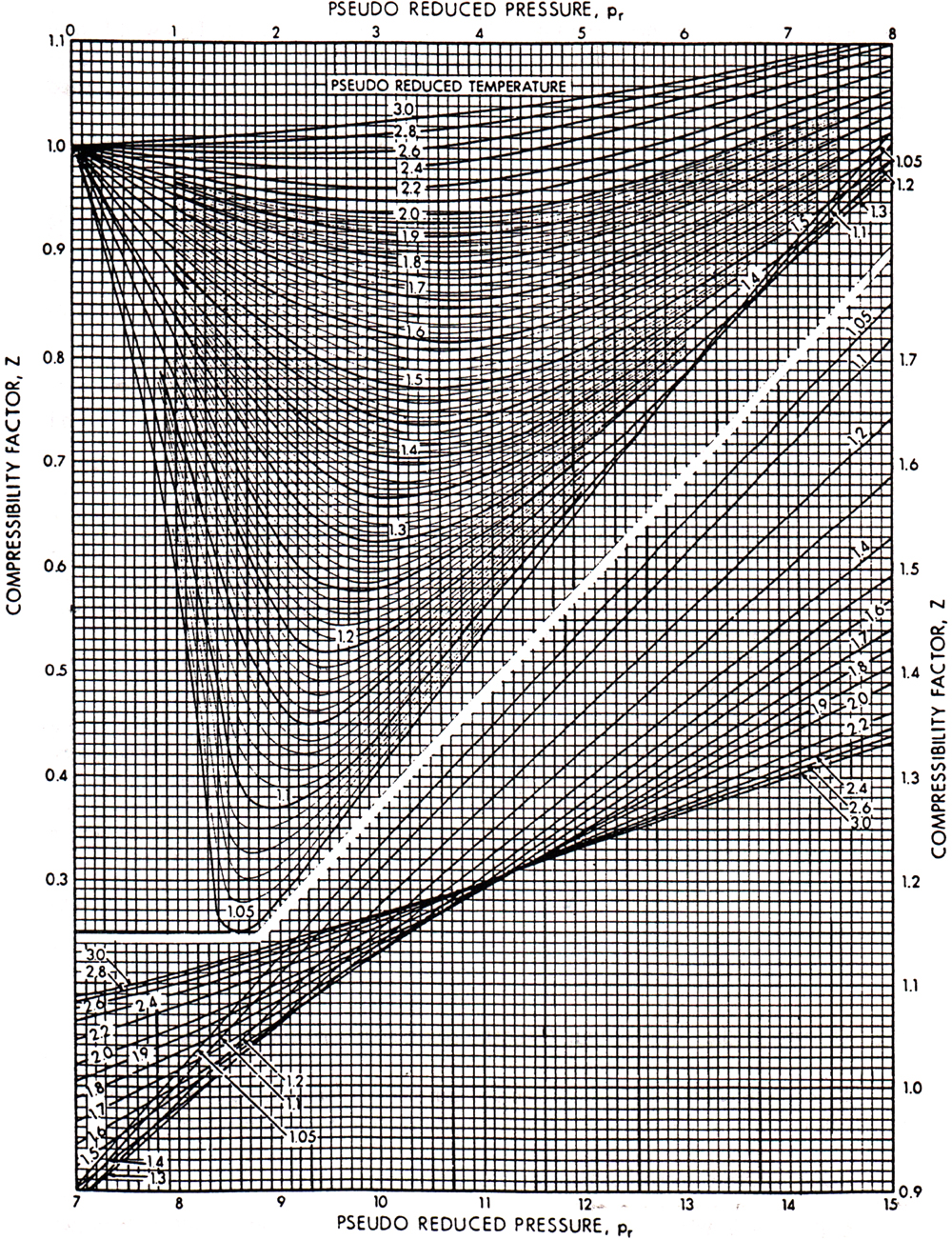
Figure 4-1. The gas deviation factor for natural gases. (From Standing and Katz, 1942.)

To use Figure 4-1 it is necessary to calculate the pseudoreduced properties (pressure and temperature) of the mixture. These properties are simply

and

where p_pc and T_pc are the pseudocritical pressure and temperature of the mixture, respectively. The temperature must be absolute (R or K), which is simply °F + 460 or °C + 273.

Several researchers have developed analytical equations to reproduce the Standing and Katz Z-factor charts. Comparative studies have shown that the Dranchuk and Abou-Kassem (1975) correlation is accurate to better than 1% for a wide range of temperatures and pressures. This correlation, as presented by McCain (1990), is:

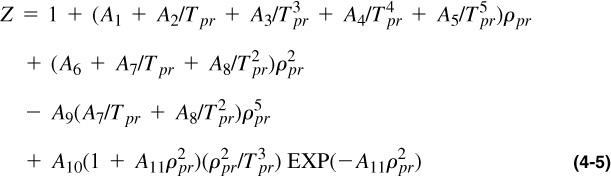
where

The constants are as follows: A₁ = 0.3265, A₂ = –1.0700, A₃ = –0.5339, A₄ = 0.01569, A₅ = –0.05165, A6 = 0.5475, A7 = –0.7361, A8 = 0.1844, A9 = 0.1056, A₁₀ = 0.6134, A11 = 0.7210.

The range of applicability is

0.2 ≤ p_pr < 30 for 1.0 < T_pr ≤ 3.0

and

p_pr < 1.0 for 0.7 < T_pr < 1.0.

Finally, as can be seen from Figure 4-1, at the standard conditions of p_sc = 14.7 psi and T_sc = 60°F = 520°R, the gas compressibility factor, Z_sc, can be taken as equal to 1.

---

Example 4-2. Use of the Real Gas Law to Calculate the Volume of a Gas Mixture at Reservoir Conditions

Assume that a natural gas has the following molar composition (this is the fluid in the reservoir described in Appendix C): C₁ = 0.875, C₂ = 0.083, C₃ = 0.021, i-C₄ = 0.006, n-C₄ = 0.002, i-C₅ = 0.003, n-C₅ = 0.008, n-C₆ = 0.001, and C₇+ = 0.001.

Calculate the volume of 1 lb-mol of this mixture at reservoir conditions of T = 180°F and p = 4000 psi.

Solution

The first step is to calculate the pseudocritical properties of the mixture. These properties are simply the summation of the individual contributions of the component gases, weighted by their molar fractions. This is based on the classical thermodynamics law for ideal mixtures and Dalton’s law of partial pressures. Table 4-2 gives the results of this calculation.

Table 4-2. Calculation of Pseudocritical Properties for Example 4-2

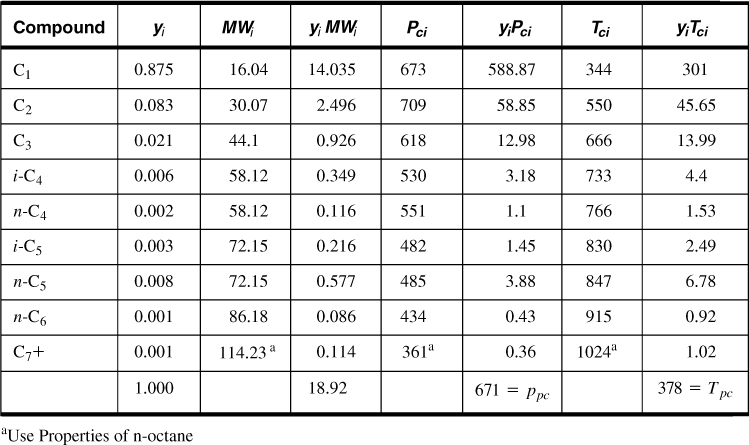
The pseudoreduced properties are then p_pr = 4000/671 = 5.96 and T_pr = (180 + 460)/378 = 1.69. From Figure 4-1, Z = 0.855. Then, from Equation (4-2) and rearrangement,

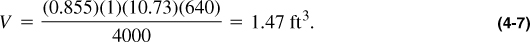
Equation (4-5) gives Z = 0.89 and V = 1.53 ft³.

---